Educational Games - make the best and most pleasant form of education.

Our educational games and exercices teach you many new thinks and by pushing your imagination and entertaining you let you develop your brain ability to deal with everyday chalanges in your school.
You will learn to think fast and effectively while gathering necessary knowledge to resolve any tasks you may have during your study. You will be able to resolve problems independently as well as make valuable contribution working with others. You will be able to learn quickly and independently. Your analitical skills allows you to understand and create formulas you may need without cramming them.
The descriptions of the games you will find are generally simplified and do not show all possibilities. We have done this to let you discover them by doing experiments. We think this can make the games more interesting. Your satisfaction from your discoveries may be more valuable then simple playing. Our actual games a are discribed below. You can expect more in the nearest future.
The author have a hope that you will enjoy the games and expects your feedback. You are encouraged to share your ideas concerning any new games we can develop or to suggeste the development of ones you may already know. It is quite possible we will make some together.
Witold Wójcik
Five dices game |
Mastered matters:
|
Dices were probably originally made from the ankle bones which are approximately tetrahedral. Recently, the use of plastics is nearly universal. It is almost impossible to trace clearly the development of dices, it is certain, however, that they were used in prehistoric times. The faces of most dices are labelled using whole numbers, starting at one. Most of dices are cubical but there are some having more sides labelled with symbols which are not numbers. Generally, all dices are used to generate a random result. Q-workshop
According to wikipedia, the game of 5 dices exerts the following probability to expect different results. They are sorted by ranking.
| Category | Probability | Percentage | one in... |
| Five of a kind | 6 / 7776 | 0.08% | 1296 |
| Four of a kind | 150 / 7776 | 1.93% | 51.8 |
| Straight | 240 / 7776 | 3.09% | 32.4 |
| Full House | 300 / 7776 | 3.86% | 25.9 |
| Three of a kind | 1200 / 7776 | 15.43% | 6.5 |
| Two pairs | 1800 / 7776 | 23.15% | 4.3 |
| One pair | 3600 / 7776 | 46.30% | 2.2 |
| Null | 480 / 7776 | 6.17% | 16.2 |
For our counting exercises which make the main purpose of our play we have set the following rules for the game:
| 5 of a kind | 1500 * combination value |
| 4 of a kind | 250 * combination value |
| 3 of a kind plus 2 of a kind | 50 * threes value plus 20 * pair value |
| 3 of a kind | 10 * combination value |
| Straight from 2 | 20 points |
| Straight from 1 | 15 points |
| Two pairs | half of the combinations value |
| One pair | half of the pair's value |
| Null | void |
The points may be accumulated for each player. The end of the game may be determined by the time of the play, the specific number of turns or by the amount of points to be reached.
The game is available in the Let's play section.
designed by Witold Wojcik
Words 1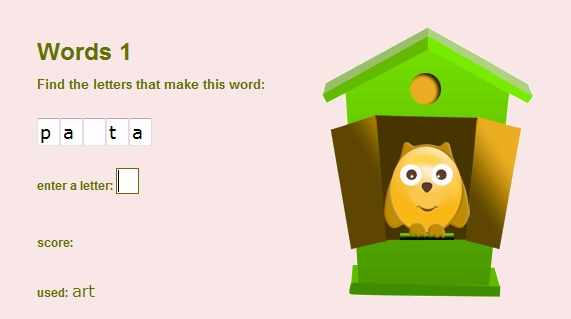 |
Mastered matters:
|
Words 1- Game description
Guess the letters that make the word. Point the mouse on the small box, click and enter your letter. If your letter is present in the word all positions it occupies will be filled with and you get a point. If your letter is not used you will lose one point.
The game is similar to the hangman but you are not stressed.
Your game is watched by an owl living in the green birdhouse. The owl lose its interest if you make mistakes.
All the letter you use are displayed for you to avoid repetitions. When the word is completed the game is over and your score is displayed.
Good luck!
The game is available in the Let's play section.
designed by Dorota Pelszyk, Witold Wojcik & Ewa Najduk
Words 2 |
Mastered matters:
|
Words 2- Game description
Your task is to guess the word and complete it with the missing letters.
To write a letter into the word put the mouse over the chosen place click and enter your letter. If the letter is good it remains at its place and you get a reward point. If your letter is wrong it is erase and you lose one point.
Your performances are observed by Matilda which shows her disagreement if you make mistake. Please do not feel offended by her simple behaviour.
The purpose of the game is to help you to improve your spelling skill. When the word is completed the game is over and your score is displayed.
Good luck!
designed by Witold Wojcik & Dorota Pelszyk
Magic Square 1 |
Mastered matters: |
Find out all the hidden numbers under the coloured fields of the magic square. All the sums in rows and columns are equal to a specific number displayed on the screen. All hidden numbers are digits.
To enter your number put the mouse over a field, click and enter your digit. If your digit is correct it remains in the field and you get one point. If your digit is wrong it is erased an you lose one point.
Your score is displayed on the screen accordingly to your performance. When the square is completed the game is over which is announced by the trumpet.
There are some hidden rules related to the use of the colours to be discovered by you, in order to get better results.
Good luck!
The game is available in the Let's play section.
designed by Witold Wojcik
Magic Square 2 |
Mastered Matters: |
Find out the numbers under the coloured fields in order to complete the square. All the sums in rows and colons are equal to a specific number. The number is displayed on the screen.
To enter a digit in a field put the mouse over it, click, then enter your digit with the keyboard. If your digit is correct it remains in the field and you get one reward point. If your digit is wrong it is erased an you lose one point. Your score is displayed on the screen accordingly to your performance. When the square is completed the game is over which is announced by a trumpet.
There are some hidden rules related to the use of the colours to be discovered by you in order to get better results.
Good luck!
The game is available in the Let's play section.
designed by Witold Wojcik
Magic Square 3 |
Masteres matters: |
Find all the numbers under the coloured fields and complete the square. The sums of digits in each row and colon are equal to a specific number displayed on the screen.
Put the mouse over a field, read the clue which appears below the magic square, click end key your digit. If you do not understand a given clue, search for information in the Math section of the website.
If your digit is correct it remains in the field and you get one reward point. If your digit is wrong it is erased an you lose one point. Your score is displayed on the screen accordingly to your performance. When the square is completed the game is over which is announced by the trumpet sound.
There is a hidden rule related to the use of colours to be discovered by you in order to get better results
Good luck!
The game is available in the Let's play section.
designed by Witold Wojcik
Wolf, goat and cabbage |
Mastered matters:
|
The Wolf, goat and cabbage brain teaser comes from the 8th century A.D. and is attributed to Alcuin, an Anglo-Saxon monk, born in York in 735, one of the leading scholars of his time.
It requires a bit of logic and non inertial thinking. It is usually solved in a few minutes by children. Does it take longer for adults?
Here is our version. A man has to take a wolf, a goat, and a cabbage across a river. While crossing the river the man can carry only one of them. Only when the man is present are the goat and the cabbage safe from their enemies. How can he do that ?
The game is available in Let's play section
designed by Witold Wojcik.
Clusters |
Mastered matters:
|
The big square 9 x 9 cells is divided into 9 smaler 3 x 3 squares called clusters. Clusters are marked with differed background. The object of the game is to fill the empty cells with numbers between 1 and 9 according to the following guidlines:
Number can appear only once on each row
Number can appear only once on each column
Number can appear only once on each cluster
Try to resolve this brainteaser you can do it on your computer or you can print it and do it on the paper.
Doing this on your computer is easier as it does not allow you to make mistakes. They are counted off course. Good luck and enjoy!
The game is available in Let's play section
designed by Witold Wojcik
Clusters for kids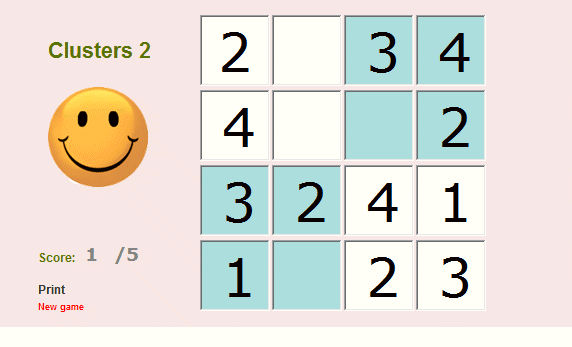 |
Mastered matters:
|
The big square 4 x 4 cells is divided into 4 smaler 2 x 2 squares called clusters. Clusters are marked with differed background. The object of the game is to fill the empty cells with numbers between 1 and 4 according to the following guidlines:
Number can appear only once on each row
Number can appear only once on each column
Number can appear only once on each cluster
This brainteaser is designed for young children. They can do it on the computer or it can be printed on the paper.
Doing this on your computer does not teach writing but is easier as the computer does not allow the player to enter a number incorrectly. Off course all mistakes are counted to produce a final score. Good luck and enjoy!
The game is available in Let's play section
designed by Witold Wojcik
Number |
Mastered matters:
|
The objective of the game is to find out a number chosen by one of the player you or your computer. You play against the computer. If it is your turn to find a chosen number you are encurage to use the natural numbers axis by pointing the coursor on it to generate a number. After your number is chosen enter it by clicking. You may also write your number into the entry field named player but then you must click the computer field to get its response.
If the computer search for the number you choses you have to click its field any time you want to get its response.
Sometimes the number can be guessed at once but the chanc eis rather small 1 to 100 but ther is a strategy while use can limit the number of trials up to seven or if you are lucky even less than that. If you find it you can conquer the computer because it does not use it. Its guesses are logical but it tries to gamble rather than use any strategy
We hope you'll enjoy it. Goot luck!
The game is available in the Let's play section.
designed by Witold Wojcik
Bingo |
Mastered matters: |

The purpose of the game is to teach small children the natural numbers up to 99 Off course the game is well known by adults and often played for plaasure.
Our game makes a perfect occasion to teach children basic number while plaing together with them.
Only the winner usualy gets the final prize agreed before the game but it is also possible to award more players by dividing the prize among them accordingly to the order they finish they cards at the ratio set for example as 60%, 30% i 10%.
Serching for numbers to be marked remember that there could be more then one specific number on a card an off course you have to check all your card concecutively.
Rules of the game:
To prepare game accessories enter player name, set quantity of cards, click [enter] then click[print cards]. Repeat this procedure for all players. Finally click[start].
player's name: Cards: [ start ]
During the game the computer randomly fetshes numbers in the range 0 do 99 and displays them.
The time between drawing is set by default to secondes. Yuo can change it any time by clicking the time showing button. The game is then suspended. You may suspend the game also any time by clicking [stop] To continue the game click [kontynuuj].
The game is available in the Let's play section.
designed by Witold Wojcik
Factors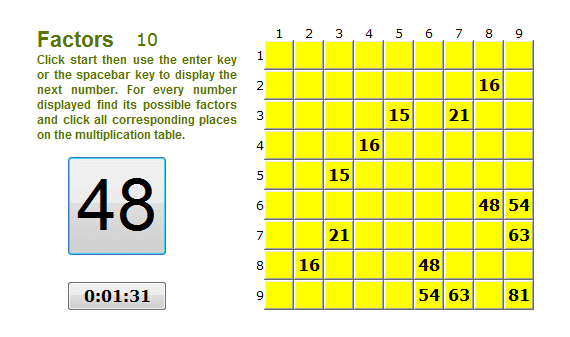 |
Mastered matters: |
The game can make you a master of multiplication. This is individual game but you can compare your best result with others by sending it to the server.
Your score depends on your speed, number of mistakes and omissions. For every mistake you get penalty secondes and the presents of omissions restricts you to become a master. Do not worry any how. Not everyone can be be a master at once. Be pation an ejoy the game and the results will follow. Send your result after the game is finished. Do not forget to enter your name.
Player name: score:
Mistakes: Omissions:
Score list:
| Player | time[sek] | degree | |
| 1 | Janek K | 310 | student |
Good luck!
The game is available in the Let's play section
designed by: Witold Wójcik

Haning fun with Math
The mathematical exercises that we develop have the purpose of teaching and entertaining. Having no intention to develop future mathematicians, we think that the positive feeling toward Mathematics is very important and can make a big difference for every pupil in the school, so we want to create it. As any other subject, Math to be easy has to be loved and to be loved must be interesting and useful.
While the calculator can do the most of a job, it is rather difficult to convince students about the relevance of understanding Mathematics. On the other hand there are too many formulas and mechanical procedures to be learn and remember. That way, it is hard to notice the beauty of Mathematics.
To change this, storing formulas should be replace by dip understanding so formulas can be easy withdrawn or ad hock created. The essence of being human is to understand the heart of the matter not to store information, which is much better done by books and computers.
By understanding things the man gets the necessary psychological equilibrium, which make him feel satisfied and important. This is relevant for our development and career. We want to give you such a feeling while introducing to you the wonder of Mathematics.
Pogrammed by Witold Wojcik
Graphics by Ewa Najduk
Comparing sets be careful, sheep can jump! |
Mastered matters:
|
Can we count without knowing numbers? It seems to be impossible. However, our ancestors were able to do it. They did not name any numbers, so how was it possible?
Yes, it is possible. As a matter of fact counting is an action of comparing. When we use numbers we compare counted elements with certain symbols said or written. Those symbols represent certain properties of sets called quantity of elements or cardinal number.
When we are comparing our set with another set we are creating pairs where each element from one set has its companion from another. This way we can make the second one (stones) equal to the first (sheep) in the sense of quantity.
In the set of stones every stone represents exactly one sheep it is not important which one but only one sheep.
Did shepherds count their sheep? Yes they did as they created a second set with the same property as the set of sheep. This common property of both sets was the quantity of the elements each one had. They got the same cardinal number.
Of course by giving every quantity a specific name or symbol to represent it we can do much better but then we have to organise those symbols by putting them in order (so as to know for any given one which one is the previous and which one is the next)
The sets of sheep and stones are much different phisically but they have one thing in common, their cardinal numbers are the same. The cardinal numbers of sets had made the concept of natural numbers as we know it.
The only remaining problem as we already mentioned was to attribute some symbols to different quantities and put them in order.
The results of this attempt were different. Here are some of them:


As we can see some symbols were designed in a way that they could represent the quantity visually. Of course it was not possible to do that for bigger numbers. Hindu an Arabs were more imaginative as they invented a positional way to represent any quantity and only ten figures were necessary to do the job. We call those figers decimal digits.
Now, Can you work out this puzzle?
A driver has a brother, but that one has no brothers. What is the driver?
designed by Witold Wójcik
Counting stones |
Mastered matters:
|
As we already mentioned, people tried to create separate symbols for all given quantity, but of course it was impossible. Because of that they started to create groups of the specific quantity and then they named them; that way Roman numbers were invented. There also existed other systems as well. Here are some examples:
Babylonian Numbers


As you can see, it would not be easy for us to remember them. Chinese figures have a very long tradition and are still in use today.
For us, they look impossible but for a well trained mind this is not a problem.
Both, Babylonians and Chinese used decimal systems by associating elements in groups of ten but the symbols they used were much different.
Hindu-Arabic numbers
We do not exactly know who made more effort to develop the decimal system. Its beginning took place in India and the final world wide distribution was done by Arabs. Of course Mathematicians from both nations contributed a lot to the development of decimal system and corresponing digits and we can say those results had changed human civilisation forever.
Here they are as they were at the beginning:

Please take a look at the picture. What clue had been given to recognize the quantity? What was zero created for? Finally, please resolve the following: How to write down the 1000 using five 9's ?
The exercice is available in the Math/Physics section.
designed by Witold Wojcik
Building number systems - Binary system |
Mastered matters: |
Grouping objects.
Group identical objects by two. Point them with the mouse and drag them to each other. The joining point of each picture is located at the top left corner. Group the objects by dragging their joining points, one over another. The program does not allow you to make a group bigger than two identical objects, neither you can group two different objects.
The principals of the positional systems.
To limit the number of necessary symbols in expressing quantity, people invented a positional representation of numbers. The system can use any chosen number of symbols (digits) as a base. Counted elements are grouped. Every completed group contains the number of objects equal to the base. New objects created by grouping can be made of smaller identical completed groups.
To represent a given quantity the numbers of different kind of completed groups has to be written down starting with the number of the biggest groups from the left to the right. If some possible groups are not present, zero is written. Finally the expression is ended by giving the number of remaining units.
The number of units, different completed groups contain, is given by the following formula:
g=bp
where g is the number of units, b is the number equal to the given base and p is the current position in the expression counted from the left to the right and started with 0 for the position of units. The number of units in the completed groups at a given position is called the weight of the position.
Example for binary system system: 1101= 1 group containing two groups of two groups of two, 1 group of 2 two groups of two, no group of two elements, and 1 units.
| 1 | 1 | 0 | 1 |
|---|---|---|---|
| oo oo oo oo |
oo oo |
o |
To understand the notations of any positional number system we have to remember, or be able to resolve using the blue formula, the weight of every position in the notation. That also can be counted knowing that each next to the left position has a weight base time bigger than the previous one.
Exercise is available in Math/Physics section.
designed by Witold Wojcik
Building number systems - Base three sysstem |
Mastered matters: |
Grouping objects.
Group identical objects by three. Point them with the mouse and drag them to each other. The joining point of each picture is located at the top left corner. Group the objects by putting their joining points, one over another. The program does not allow you to make a group bigger than three identical objects, neither you can group three different objects.
The principals of the positional systems.
To limit the number of necessary symbols in expressing quantity, people invented a positional representation of numbers. The system can use any chosen number of symbols (digits) as a base. Counted elements are grouped. Every completed group contains the number of objects equal to the base. Objects can consist of smaller identical completed groups.
To represent a given quantity the numbers of different kind of completed groups has to be written down starting with the number of the biggest groups from the left to the right. If some possible groups are not present, zero is written. Finally the expression is ended by giving the number of remaining units.
The number of units, different completed groups contain, is given by the following formula:
g=bp
where g is the number of units, b is the number equal to the given base and p is the current position in the expression counted from the left to the right and started with 0 for the position of units. The number of units in the completed groups at a given position is called the weight of the position.
Example of base three system number: 210= 2 groups of three groups of three, 1 group of three, no units.
| 2 | 1 | 0 |
|---|---|---|
| ooo ooo ooo ooo ooo ooo |
ooo |
To understand the notations of any positional number system we have to remember, or be able to resolve the weight of every position in the notation using the blue formula. That can be also counted next position to the left has its weight base time bigger than the previous one.
The exercise is available in Math/Physics section.
designed by Witold Wojcik
Building number systems - Decimal system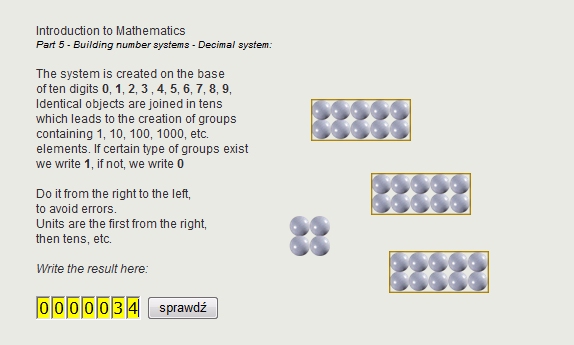 |
Mastered matters: |
Grouping objects.
Group identical objects by ten. Point them with the mouse and drag them to each other. The joining point of each picture is located at the top left corner. Group the objects by putting their joining points, one over another. The program does not allow you to make a group bigger than ten identical objects, neither you can group ten different objects.
The principals of the positional systems.
To limit the number of necessary symbols in expressing quantity, the humans invented a positional representation of numbers. The system can use any chosen number (base) of symbols (digits). Counted elements are grouped. Each group contain the same quantity of identical elements determined by the base, which can be simple units, groups of elements or groups of smaller groups.
Example from decimal system: 243= 2 groups, each containing 10 groups of ten elements, 4 groups of ten elements and 3 units.
| 2 | 4 | 3 |
|---|---|---|
|
oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo oooooooooo |
oooooooooo oooooooooo oooooooooo oooooooooo |
ooo |
The exercise is available in Math/Physics section.
designed by Witold Wojcik
Can numbers have shapes? |
Mastered matters: |
- Let's examine some properties of numbers
It is rather difficult to associate shapes with numbers. However, mathematicians, while examining numbers, discovered several interesting phenomena. If we put identical objects like balls one close to an other, such sets can be organised in different geometric shapes like triangles, squares, rectangles, etc.
To obtain any given shape some specific numbers of elements must be used. Supported by such phenomenon we can say about numbers to be triangular, square, etc. accordingly to the shapes they can be aranged in.
Of course we can also put objects ones on the top of others creating prisms, cubes and other 3 dimensional objects. What is interesting, we always must use some specific numbers of elements to obtain some specific shapes..
In the exercise we are above to do two different algorithms will be used. The first one will try to build triangles at the left side of the window, while the second one will try to build squares at the right side of the screen. For what numbers they can succeed ? Let's find out using + and - buttons.
Enjoy!
Can any given number be triangular and square at the same time? What do you think?
Maximal number of balls is 210
The exercise is available in Math/Physics section.
designed by Witold Wojcik
Three dimensional numbers? - Let's examine their properties |
Mastered matters: |
The cube appearing in the window above is built with 216 balls. You can obtain many other shapes by removing some of the balls it contains. To do so you have to chose a ball, point it with the mouse and click it.
If you accidentally remove a wrong ball you can make it reappear by clicking the [ back ] button
Removing some balls, try to built different regular 3D shapes you know and then check the number of the balls used. The actual quantity of the balls used is shown all the time by the counter on the left top side of the window.
After creating some regular shapes, try to calculate the number of the balls in use by applying some known formulas for the volume count.
Enjoy!
The exercise is available in Math/Physics section.
designed by Witold Wojcik
Creating more 3D shapes |
Mastered matters: |
 The cube above can be modified by removing balls. To remove a ball point on it with the mouse and click. If you have removed wrong ball you can make it reappear again using [back] button. To remove balls from the other sides of the cube turn it using [turn] button.
The cube above can be modified by removing balls. To remove a ball point on it with the mouse and click. If you have removed wrong ball you can make it reappear again using [back] button. To remove balls from the other sides of the cube turn it using [turn] button.
You can resolve the number of the balls used by applying the formulas you usually use for the volume count.
Enjoy.
The exercise is available in Math/Physics section.
designed by Witold Wojcik
Addition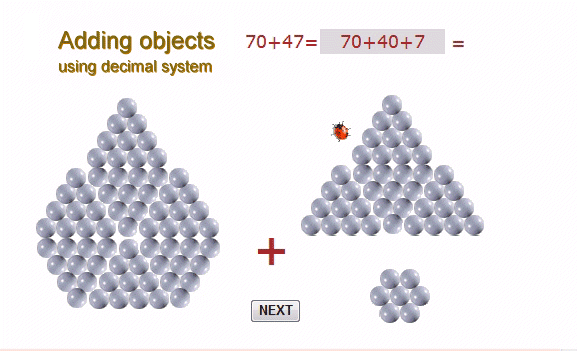 |
Mastering Matters: |
Addition of natural numbers is very simple. We add them like we add objects so final results are independent of the how we do it. Addition of numbers expressed in decimal system is simple and can be more efficient by making addition in groups acordingly to the system. Generally off course the order of adding numbers does not matter.
In practis adding objects for example does not recquire any special ruls. It does not matter how they are placed all together except they are create one set but if the question "How many ? " arise we have to group them or count them then use our symbolic method of expresing quantity. It means that to answer this question we have to make order phisycaly or mentally with our set.
We know that to expres quantity in our decimal system we have to group object by tens, hundreds, thousants etc. What is remaining are units. While adding numbers to keep better order we add similar groups first. It is easier than to put them in order.
Our exercise two numbers to be added are shown as two sets of objects. The computer does not allow you to add different decimal groups so the rules of adding those objects are identical as to the rules off adding decimal numbers.
the bills are arange in figures in order to recognize the related quantity. The groups can be moved by draging and dropping with a mouse Rysunki można przesuwać. You can join similar groups by puting one over an other.
Enjoy!
The exercise is available in Math/Physics section.
designed by Witold Wojcik
Adding natural numbers |
Mastered matters: |
To add the numbers you have to separate groups units tens hundreds etc. You can do it by dragging and dropping them with the mouse. Then you can add similar groups all together by aproaching one to an other an eventualy clicking on them.
After "graphical" adition is finished you can write down the result in the text field input just after = sign. If you do not want to play with figures you can write the result at once. To check your answer is correct click on the elephant.
Enjoy!
The exercise is available in Math/Physics section.
designed by Witold Wojcik
Addition Algorithm |
Mastered matters: |
To obtain the result of addition add all the digits in consecutive columns starting with the column of units (First on the right) If the result of a such addition has only one digit put it under the bottom line if it has more write down the last one and put other digits on the top of the pile of numbers you are adding acordingly to their weight, so tens to tens etc. Because they are to be added to the next column of digits and they are generated by the previous one in the decimal number system we call them decimal carry.
You can also remember those digits. Any way you proceed you have to add them to the next column while you are adding it.
Doing our exercice you will try to remeber carries. To exercise writing them down click [HELP]
Enjoy!
The exercise is available in Math/Physics section.
designed by Witold Wojcik
Substruction Algorithm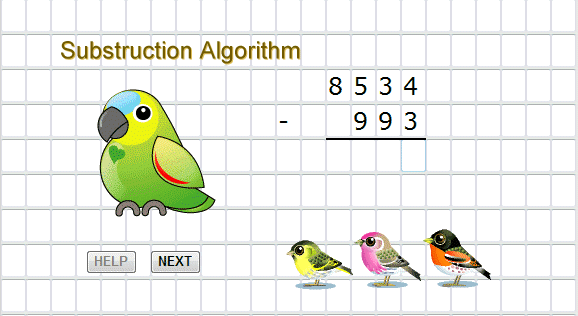 |
Mastered Matters: |
While adding numbers we can procede on a large pile of them but to do substruction it is better to do it in twos. It can be done by adding all negative ones (to be substructed) all together first. Example: 3745-740-1020-15= 745-(740+1020+15).
It is presumed that the substruction algorithm differ significantly from that of addition but it is not the case. Off cours intead of adding digits we substruct them and instead of adding carries we substruct the as well. If we understand this process both algorithms seems to be identical.
So to get the result of any given substruction we write the number to be substruct under the one which we have to substruct from then we substruct consecutively the digits in columns starting with the first on the righr, means units and write down the results under the bottom line.
If the top digit is to small we add 10 to it and write down the result. This ten is our decimal carry take off course from the next column on the left so if we want to write it as usual on the top of the pile we do it by puting -1 above the next column. If you prefer to remember that you have take 1 from the next column without writting it it is OK too.
So you repet this procedure for all columns one after an other remembering or writting our negative carries.
Doing our exercices you will try to remember them to train your memory but if you want to exercise writing click [HELP].
Enjoy!
The exercise is available in Math/Physics section.
designed by Witold Wojcik
Multiplication by adding |
Mastered matters: |
Multiplication can be replace by addition but it is better to use appropriate algorithm. To be able to use algorithm we have to master the results of multiplication of natural numbers in the range of 1 to 9. We will do it later but now we try to understan the nature of multiplication.
The result of multiplication of two natural numbers let's say A and B can be be expressed by a rectangle having A row and B columns or vice versa. This bring instantly an idea that A x B is the same as B x A.
In our exercise we set the number of columns to be equal to the first to A and the number of rows to be B. This means that if we got for example 7 x 3 we should pain 7 squares in the first row then paint next two rows in the same manner to get the total 3 rows for 7 square each.
The small square can be counted but you may get the result by clicking the last one on the bottom right. The computer will count all correctly pained squars an also the wrong ones. For every right pained square the p-layer gets 1 point and for the wrong one -1 point. If there are more negative points than the right one the resulting score is 0.
Your cumulative score as well as the score obtained in the last exercises in () are shown in the small window. The time of exercise is mesured by the timer.
Enjoy!
The exercise is available in Math/Physics section.
designet by Witold Wojcik
Multiplication Algorythm |
Mastered Matters: |
We start doing this exercises by multiplying a few digits number by a one digit number.
We do it by multiplying all concecutive digits of the biger number by that digits. We star with the last one then tens and so on. units. The results are written below the bottom line under the corresponding columns of the bigger number. When a single result of multiplication is bigger then ten this generate a decimal similarely as in additions and this carry is then added to the next column multiplication result and so on.
The procedure is repeateduntil the last column is multiplied an the result is written.
Let's make an example: 6127 * 3 = ( 7 + 20 + 100 + 6000 ) * 3
wykonujemy kolejno 7 * 3 + 20 * 3 + 100 * 3 + 6000 * 3
otrzymując: 21 + 60 + 300 + 18000 = 18381
We can show this like follows:
| multiplications | products | ||||||
| 7*3 | 2 | 1 | |||||
| 20*3 | 6 | 0 | |||||
| 100*3 | 3 | 0 | 0 | ||||
| 6000*3 | 1 | 8 | 0 | 0 | 0 | ||
| Total: | 1 | 8 | 3 | 8 | 1 | ||
If we give up writtin the last zeros but remember to shift left concecutive results we get this:
| multiplication | products | ||||||
| 7*3 | 2 | 1 | |||||
| 2*3 | 6 | ||||||
| 1*3 | 3 | ||||||
| 6*3 | 1 | 8 | |||||
| total: | 1 | 8 | 3 | 8 | 1 | ||
the product of 7*3 is a two digit numbers and 2 is a decimal carry to added in the next column. Similarely the multiplication 6*3 gives a carry equal 1. Carries may be memorized and added i the following columns or may be written. If there is no more columns like after multiplication 6*3 and ther is a decimal cary both figures can be written at the beginning of the result.
The schematic of the multiplication can be farther simplify as follows:
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
After you have mastered this one digit multiplication procedure you can increace the number of digits in the second number by clicking the left button.
All the procedures are the same exept that we have to find result for every digit of the second number. We start with its units then tens and so on. The results are written one under un other but we shift every next result by one digit left. Then we adding them. Off cours we have to handle decimal carries as well.
The method will be explaine on the following example:
1030 * 431 = 1030 * ( 1+30+400) wykonujemy kolejno 1*1030 + 30*1030 + 400*1030
We got: 1030 + 30900 + 412000 = 443930 which is the final result.
Let's show this this way:
| multiplications | products | ||||||
| 1*1030 | 1 | 0 | 3 | 0 | |||
| 30*1030 | 3 | 0 | 9 | 0 | 0 | ||
| 400*1030 | 4 | 1 | 2 | 0 | 0 | 0 | |
| total: | 4 | 4 | 3 | 9 | 3 | 0 | |
This method differ by that that we shifted the results instead of writing final zeros. Let's have a look:
| multiplications | products | ||||||
| 1*1030 | 1 | 0 | 3 | 0 | |||
| 3*1030 | 3 | 0 | 9 | 0 | |||
| 4*1030 | 4 | 1 | 2 | 0 | |||
| total: | 4 | 4 | 3 | 9 | 3 | 0 | |
Good luck and enjoy!
The exercise is available in Math/Physics section.
designed by Witold Wojcik
The page you are currently watching has only informational purpose. the games an exercises do not function on thi page. To make use of them you have to click [Let's Play] or [Math/Physics] in the main and then choose right game or exercise from the provided submenus.